LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA GIMNAZJUM

Zadanie 4

Dany jest kwadrat o boku długości 4 cm. Z każdego wierzchołka jako ze środka skonstruowano koło o promieniu 4 cm. Znaleźć pole figury będącej częścią wspólną tych kół.

Rozwiązanie



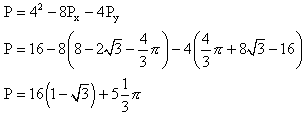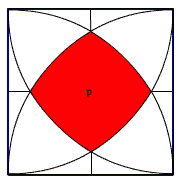
  • Oznaczam  wspólne pole czterech kół literą P.
  • Z dolnej krawędzi kwadratu konstruuję trójkąt równoboczny. Z tw. Pitagorasa jego wysokość jest równa 

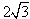
  • Poniżej obliczam:

       pole trójkąta: Pt
       pole wycinka koła (30o): Ps
       pole obszaru oznaczonego literą x:  Px

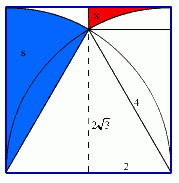
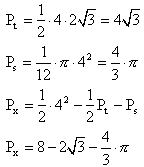
        Obliczam pole x

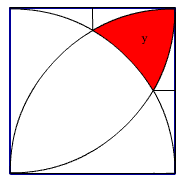
     Obliczam pole obszaru oznaczonego literą y:   Py

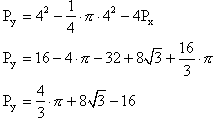
       obliczam pole y

     Obliczam pole P

       obliczam pole P

Autor:Radek Mastalerz