LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA SZKÓŁ PODSTAWOWYCH
zadanie nr 19
Czy można na okrągłym talerzu o promieniu 10cm umieścić prostokątny tort o wymiarach 8cm i 28cm przecinając go nożem wzdłuż prostej na dwa kawałki?
Okazuje się, że można, chociaż to zadanie sprawiło mi wiele problemów.
Ale zacznijmy od początku.
najpierw sprawdźmy czy rzeczywiście możliwe jest, że w ogóle ten tort zmieścił się na talerzu
w takim razie talerz musi mieć większą powierzchnię
Po-pole talerza
Pt-pole, jakie zajmie na talerzu tort
Po=3,14*r 2
Po=3,14*100="314
Pt=28*8="=224
więc rzeczywiście talerz ma większa powierzchnię
pozostaje tylko pytanie "czy można położyć go na talerzu, przekrajając go tylko raz wzdłuż linii prostej?"
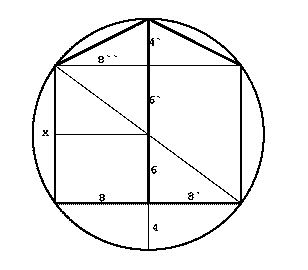
Można, ja wymyśliłem następujący sposób:
(nie przejmujcie się tymi "`" przy cyfrach - po prostu nie mogłem wstawiać takich samych ciągów znaków)
Postanowiłem pokroić tort ukosem na dwa identyczne trapezy prostokątne i złączyć dłuższymi podstawami, o tak:
Na rysunku to już widać, ale na początku nie wiedziałem, w jakim miejscu zacząć krojenie. W tym celu musiałem policzyć x
162+x2=202
x2=400-256
x2=144
x="12
no dobra
teraz sprawdzam czy pola tych kawałków zgadzają się
Pk-pole protokąta (tego z czarnymi krawędziami)
Pt-pole trójkąta (tego z czarnymi krawędziami)
Pk=12*16="160+32=192
Pt=2*(0,5*8*4)=2*16="32
32+192="=224
jak widać tort przekrojony w taki sposób mieści się na talerzu
jeśli nie wierzycie to sprawdźcie!!!
Autor:Radek Mastalerz