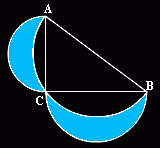
Dany jest trójkąt prostokątny ABC, w którym |<C|=90o, |AC|=3 cm, |BC|=4 cm. Oblicz obwód i pole figury, której brzeg składa się z półokręgów zbudowanych na bokach AB, AC i BC jak na rysunku.
LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA GIMNAZJUM
ZADANIE 20
| Treść zadania: Dany jest trójkąt prostokątny ABC, w którym |<C|=90o, |AC|=3 cm, |BC|=4 cm. Oblicz obwód i pole figury, której brzeg składa się z półokręgów zbudowanych na bokach AB, AC i BC jak na rysunku. |
 |
Rozwiązanie:
obliczamy pole:zredagował: Rafał Mastalerz (blizniak@viper.pl)