LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA GIMNAZJUM
ZADANIE 15
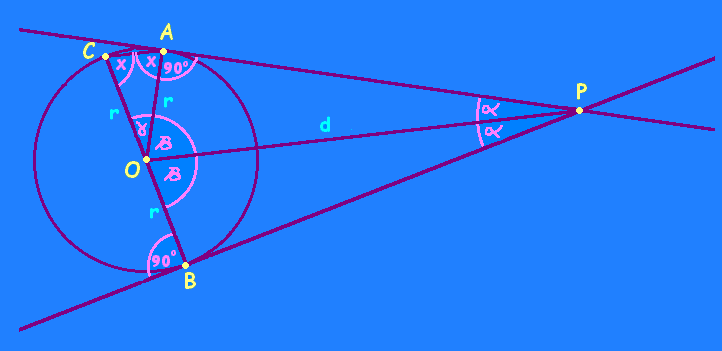
Z punktu P leżącego na zewnątrz okręgu o środku O poprowadzono styczne do tego okręgu. Punktami styczności tych
stycznych z okręgiem są punkty A i B. Następnie poprowadzono
średnicę z punktu B, drugim jej końcem jest punkt C. Uzasadnić, że prosta CA jest równoległa do prostej PO.
Trójkąty OBP i OAP są przystające na podstawie
cechy bbb. Stąd miary kątów BOP i POA są równe. Oznaczmy je b. Miara kąta g jest równa
180o - 2b, a ponieważ trójkąt AOC
jest równoramienny, oznaczając przez x miary kątów przy jego podstawie,
otrzymamy następujące równanie:
2x + 180o - 2b = 180o
2x - 2b =
0
2x = 2b
x = b
Stąd wynika, że prosta PO jest równoległa do prostej
CA ponieważ kąty naprzemianległe są tej samej miary.
Monika
Rolnicka