LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA SZKÓŁ PODSTAWOWYCH
Zadanie 15
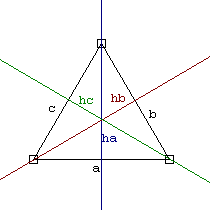
Czy istnieje trójkąt, którego wysokości mają długości: 1cm, 1/2cm, 1/3cm?
Rozwiązanie
Przypuśćmy, że:
ha = 1cm
hb = 1/2cm
hc = 1/3cm
1/2aha = 1/2bhb /*2
aha = bhb
a*1 = b*1/2 /*2
b = 2a
1/2aha = 1/2chc
aha = chc
a*1 = c*1/3
c =3a
Zauważmy:
Bardzo ważne:
Warunek wykonalności konstrukcji trójkąta
Suma długości dowolnych dwóch boków trójkąta musi być większa od długości trzeciego boku.
Z tego wynika, że nie istnieje taki trójkąt.
Alicja
