Dla trójkąta ABE
x2+42=a2
x2=a2-42
x2=a2-16
Dla trójkąta ABD
a2+b2=122
a2+b2=144
Dla trójkąta AED
x2+82=b2
x2=b2-82
x2=b2-64
Jeżeli x2=a2-16 i x2=b2-64 to
b2-64="a
b2-a2=48
A więc
b2+a2=144
b2-a2=48
2b2=192 /:2
2a2=96 /:2
b2=81
a2=48
LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA GIMNAZJUM
|
Posługując się twierdzeniem Pitagorasa można sformułować kilka wniosków:
Dla trójkąta ABE x2+42=a2 x2=a2-42 x2=a2-16 Dla trójkąta ABD a2+b2=122 a2+b2=144 Dla trójkąta AED x2+82=b2 x2=b2-82 x2=b2-64 Jeżeli x2=a2-16 i x2=b2-64 to b2-64="a b2-a2=48 A więc b2+a2=144 b2-a2=48 2b2=192 /:2 2a2=96 /:2 b2=81 a2=48 |  |
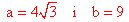 .
.