LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA KONKURSOWE Z ETAPU II
DLA GIMNAZJUM
ZADANIE 1
Pole równoległoboku ABCD jest równe 28cm2.
Na prostej CD poza równoległobokiem obrano punkt E.
Oblicz pole trójkąta ABE.
Rozwiązanie
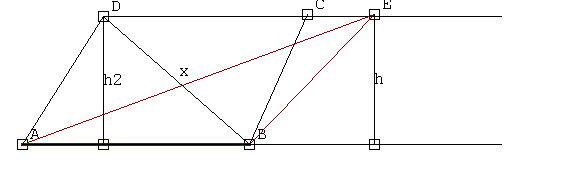
Jeżeli z punktu D do punktu B poprowadzimy przekątną x, to otrzymamy dwa trójkąty.
Ponieważ boki AB i DC są równoległe, kąty ABD i BDC są przystające i kąty BAD i BCD są przystające.
Z cechy KĄT BOK KĄT trójkąty ABD i BCD są przystające. Pole równoległoboku
jest równe 28 cm2 , więc pole trójkąta ABD wynosi 14 cm2.
Wzór na pole trójkąta to wysokość razy podstawa podzielone przez dwa. Wysokość h2
równa się wysokości h. Trójkąty ADB i ABE mają tą samą postawę i równe wysokości.
Jeżeli pole trójkąta ADB wynosi 14 cm2 to pole trójkąta
ABE również wynosi 14 cm2.
Jarek
