LIGA ZADANIOWA UMK W TORUNIU 1999/2000
ZADANIA KONKURSOWE Z ETAPU III
DLA GIMNAZJUM
Zadanie 4
Na okręgu wybrano pięć różnych punktów P,P1,P2,P3 i P4 takich że miary
kątów P1 P P2,P1 P P3,P2 P P4 są równe 45 stopni. Uzasadnij, że punkty
P1 P2 P3 i P4 są wierzchołkami kwadratu.
Rozwiązanie
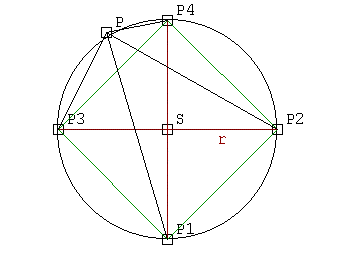
Z założenia:
kąty
P1 P P2,
P1 P P3
P2 P P4 mają po 45o.
Kąt P1 P P2 jest oparty na tym samym łuku co kąt P1 S P2, a więc z zależności która
mówi, że kąt środkowy jest dwa razy większy niż kąt wpisany oparty na tym samym łuku
: kąt P1 S P2 ma miarę 90o.
Analogicznie inne kąty mają te same własności.
Jeżeli |< P1 P P3|=45o to |< P1 S P3|=90o.
Podobnie jeżeli |< P2 P P4|=45o to kąt |< P2 S P4|=90o.
Z powyższego wynika, że kąty przy punkcie S są równe 90o.
Długość odcinka r, który jest promieniem - jest stała.
W ten sposób otrzymujemy cztery identyczne trójkąty równoramienne.
Kąty przy podstawach w trójkącie równoramiennym mają te same miary.
Jeżeli wiemy, że jeden kąt w takim trójkącie ma miarę 90o, to dwa
pozostałe mają po 45o. Przy punktach P1 P2 P3 P4 mamy po dwa kąty 45o,
czyli przy każdym punkcie mamy po 90o, a więc punkty P1 P2 P3 P4 są wierzchołkami kwadratu.
Jarek
