LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

Zadanie 1

Długości boków trójkąta są równe 12cm, 16cm i 20cm. Wyznacz najkrótszą wysokość tego trójkąta oraz środkową poprowadzoną do boku o długości 16cm.

Rozwiązanie

1) Sprawdzam czy trójkąt jest prostokątny stosując:

TWIERDZENIE ODWROTNE DO TWIERDZENIA PITAGORASA
Jeżeli w trójkącie długości boków: a, b, c są takie, że c2=a2 + b2, to trójkąt jest prostokątny oraz boki a i b są przyprostokątnymi, a bok c jest przeciwprostokątną

122 + 162 = 400 i 202 = 400 więc 122 + 162 = 202

Widzimy, że a=16, b=12 i c=20 równanie c2=a2 + b2 jest spełnone, więc trójkąt jest prostokątny.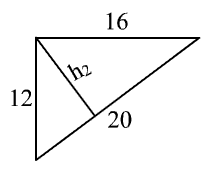
Rozmiar: 1501 bajtów
2) Obliczam pole trójkąta.

P =  a1 . h1
2
a1 = 12cm       h1 = 16cm
P =  12cm . 16cm
2
P =  192cm2
2
P = 96cm2


3) Obliczam najkrótsza wysokość trójkąta.

h2 =  P . 2
a2
a2 = 20cm
h2 =  96cm2 . 2
20cm
h2 =  192cm2
20cm
h2 = 9,6cm


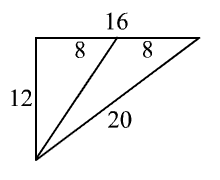
4) Obliczam środkową trójkąta do boku o długości 16cm.
Rozmiar: 1576 bajtów

Rozmiar: 1533 bajtów


Odpowiedź
Najkrótsza wysokość tego trójkąta wynosi 9,6cm, a środkowa trójkąta do boku o długości 16cm wynosi Rozmiar: 964 bajtów.