LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie 1
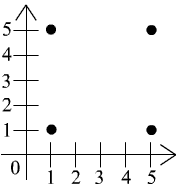
Czy zbiór {(1,1}, (1,5), (5,5), (5,1)} ma osie symetrii? Jeśli ma on osie symetrii, to napisać równania wszystkich jego osi symetrii.

Rozwiązanie


1) Obliczam odległości pionowe i poziome między punktami:

• a)(1,1) i (1,5)
  5 - 1 = 4
  
• b) (1,1) i (5,1)
  5 - 1 = 4
  
• c) (5,1) i (5,5)
  5 - 1 = 4
  
• d) (1,5) i (5,5)
  5 - 1 = 4
  

2) Odległości pionowe i poziome między wszystkimi punktami są równe 4.
3) Po połączeniu punkty tworzą wierzchołki kwadratu.

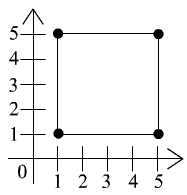
4) Każdy kwadrat ma 4 osie symetrii ( dwie są przekątnymi, a dwie pozostałe połączeniem środków przeciwległych boków).

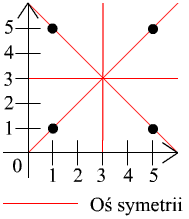
5) Zrysunku odczytuję równania osi symetrii.

lp.	Równanie osi symetrii
1	x = y   ¤
2	y = -x + 6   \
3	x = 3   |
4	y = 3   __

Odpowiedź
Zbiór ten posiada 4 osie symetrii o następujących równaniach: x = y,  y = -x + 6,  x = 3  i  y = 3 .

Mariusz Banach