Rozwiązanie
| P rombu = 3a2+ab I przekątna = 2a II przekątna = x | 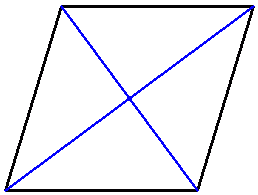 |
| P=" | 2a . x |
| . 2 |
2 |
| x=" | 2P |
2a |
| x=" | 2 . (3a2 + ab) |
2a |
| x=" | 2 . (3a2 + ab) |
2a |
| x=" | 2 . 3a2 |
+ | 2 . ab |
2a |
2a |
Druga przekątna rombu na długość 3a + b.
LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS I GIMNAZJUM
Rozwiązanie
| P rombu = 3a2+ab I przekątna = 2a II przekątna = x |  |
| P=" | 2a . x |
| . 2 |
2 |
| x=" | 2P |
2a |
| x=" | 2 . (3a2 + ab) |
2a |
| x=" | 2 . (3a2 + ab) |
2a |
| x=" | 2 . 3a2 |
+ | 2 . ab |
2a |
2a |