Jeśli przyjmiemy za podstawę a bok długości 8 cm, to wysokość h pokrywa się z bokiem długości 6 cm.
a = 8, h = 6
PD = (1/2).a.h
PD = (1/2).8.6
PD = 24
LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Zadanie 2
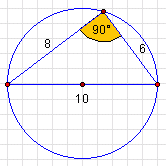
Wierzchołki trójkąta o bokach długości 6 cm, 8 cm, 10 cm leżą na okręgu o promieniu 5 cm. Oblicz pole tego trójkąta.
Rozwiązanie
| Ponieważ 62 + 82 = 102
więc z tw. odwrotnego do tw. Pitagorasa wynika, że dany trójkąt jest prostokątny. Jeśli przyjmiemy za podstawę a bok długości 8 cm, to wysokość h pokrywa się z bokiem długości 6 cm. a = 8, h = 6 PD = (1/2).a.h PD = (1/2).8.6 PD = 24 |  |
Odpowiedź
Pole trójkąta jest równe 24 cm2.