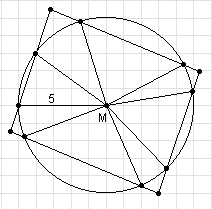
Zadanie sprowadza się do pytania:
w ilu punktach maksymalnie okrąg może przecinać sie z równoległobokiem?
Na rysunku obok widać okrąg, który przecina się z równoległobokiem w 8 punktach.
LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ETAP IV
ZADANIA NIESPODZIANKI
DLA KLAS VI SZKÓŁ PODSTAWOWYCH I KLAS I GIMNAZJUM
 |
Wszystkie punkty, których odległość od punktu M jest równa 5 cm, tworzą okrąg o środku M i promieniu 5 cm.
Zadanie sprowadza się do pytania: w ilu punktach maksymalnie okrąg może przecinać sie z równoległobokiem? Na rysunku obok widać okrąg, który przecina się z równoległobokiem w 8 punktach. |