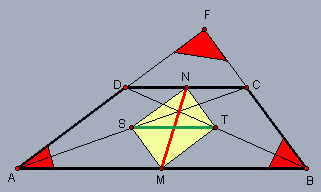
S - środek przekątnej AC
T - środek przekątnej BD
F - punkt przecięcia się przedłużeń ramion trapezu.
Pokażę, że czworokąt MTNS jest prostokątem.
LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA KONKURSOWE ETAPU IV
DLA KLAS II GIMNAZJUM
 |
Przyjmijmy oznaczenia jak na rysunku, tzn. dodatkowo:
S - środek przekątnej AC T - środek przekątnej BD F - punkt przecięcia się przedłużeń ramion trapezu. Pokażę, że czworokąt MTNS jest prostokątem. |