Tytuł

LIGA ZADANIOWA UMK W TORUNIU 2000/2001

ZADANIA KONKURSOWE ETAPU IV
DLA KLAS II GIMNAZJUM

Zadanie 5

W kwadracie ABCD o boku długości 5 cm obrano na bokach AB i BC odpowiednio punkty E i F tak, że |EB|=|FC|=1 cm. Niech G będzie punktem przecięcia odcinków AF i DE. Wyznaczyć kąt EGF.

Rozwiązanie

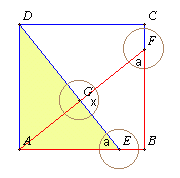|<)DAB| = |<)ABC| = |<)BCD| = |<)CDA| = 90^o
|AB|=|BC|=|CD|=|DA|=5cm
|AE|=|BF|=4cm
|<)AED| = a
Trójkąty AED i ABF są przystające bo mają boki tej samej długości, więc
|<)AFB| = a
|<)BEG| = 180^o - a
a + |<)BEG| = 180^o

Suma kątów wewnętrznych każdego czworokąta równa się 360^o.
Można to wykorzystać do obliczenie miary x szukanego kąta EFG w czworokącie EGFB.
a + |<)BEG| + |<)EBC| + x = 360^o
180^o + 90^o + x = 360^o
x = 360^o - 180^o - 90^o
x = 90^o

Odpowiedź

Kąt EGF równa się 90^o

Agata Kapica