
LIGA ZADANIOWA UMK W TORUNIU
2000/2001
Prezent wakacyjny
Zadanie 7
Wyznaczyć wszystkie liczby trzycyfrowe, które są 11 razy większe od sumy swoich cyfr.Rozwiązanie:
Dane w zadaniu można zapisać w ten sposób:
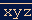 można przedstawić jako 100x+10y+z. Wstawiam to do równania.
można przedstawić jako 100x+10y+z. Wstawiam to do równania.
100x+10y+z="11·(x+y+z)
100x+10y+z="11x+11y+11z" /-10y
100x+z="11x+y+11z" /-z 89x="10z+y x,y,z € {0,1,2,3,4,5,6,7,8,9} Najmniejszy możliwy wynik 89x jest wtedy, gdy x="1 czyli 89·1="89,
a największy gdy x="9 czyli 89·8="801. Skoro 89x="10z+y to 89x € {89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99}. Z tego powodu z="8,a y="9, bo Skoro x="1, z="8 i y="9 to Karolina Kapica
Liczby x,y,z należą do zbioru {0,1,2,3,4,5,6,7,8,9}
x nie równa się 0,
ponieważ gdyby x="0" to liczba
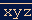 nie byłaby trzycyfrowa
nie byłaby trzycyfrowa
z nie równa się 0,
ponieważ gdyby z="0, to wtedy 10·0+y="0+y=y czyli liczba jednocyfrowa, a skoro
x nie równa się 0 to wtedy ta równość by się nie zgadzała.
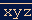 =198.
=198.