LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
ZADANIE 8
Na zewnątrz trójkąta prostokątnego równoramiennego o przyprostokątnej długości 4 cm zbudowano kwadraty. Jednym z boków każdego kwadratu jest bok tego trójkąta. Punkty przecięcia przekątnych kwadratów wyznaczają trójkąt. Oblicz pole otrzymanego trójkąta.
ROZWIĄZANIE
| Pole otrzymanego trójkąta EFC jest równe połowie iloczynu długości podstawy i wysokości (a×h)/2,
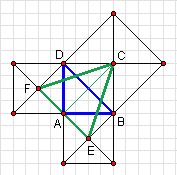
gdzie a = |EF| i h = |AC|. Pole kwadratu ABCD jest równe połowie iloczynu jego przekatnych (p×p)/2, gdzie p = |BD| = |AC|. | |
Ponieważ a = h = p, więc pole trójkąta EFC jest równe polu kwadratu ABCD. Z drugiej strony pole kwadratu ABCD jest równe 16 cm2, bo długość jego boku wynosi 4 cm. Stąd pole trójkata EFC jest równe 16 cm2. |
 |
Ewa Kocyk