Długość boku kwadratu o obwodzie 40 cm jest równe 10 cm. Każdy inny prostokąt o tym samym obwodzie możemy otrzymać wydłużając szerokość kwadratu o pewną długość x i skracając wysokość kwadratu o tę samą długość x.
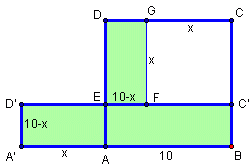
PABC'D' = PABC'FGDE < PABCD
LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA KONKURSOWE Z ETAPU III
DLA KLAS I GIMNAZJUM
ZADANIE 4
Wśród wszystkich prostokątów o obwodzie 40 cm wyznacz ten, który ma największe pole. Odpowiedź uzasadnij.ROZWIĄZANIE
Długość boku kwadratu o obwodzie 40 cm jest równe 10 cm. Każdy inny prostokąt o tym samym obwodzie możemy otrzymać wydłużając szerokość kwadratu o pewną długość x i skracając wysokość kwadratu o tę samą długość x. |
 PABC'D' = PABC'FGDE < PABCD |
| W ten sposób otrzymamy prostokąt o bokach 10+x i 10-x. Jego pole jest równe (10+x)×(10-x) = 100 - x2 i oczywiście jest mniejsze od pola kwadratu równego 100 cm2. | |
ODPOWIEDŹ
Wśrod prostokątów o obwodzie 40 cm największe pole ma kwadrat.