LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

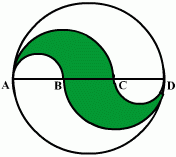
Oblicz pole i obwód zacieniowanej figury, gdzie występujące łuki są półokręgami oraz |AB|=|BC|=|CD|=3 cm.

Rozwiązanie

Jeśli odbijemy symetrycznie dolną część zacieniowanej figury, to otrzymamy figurę o tym samym polu i obwodzie.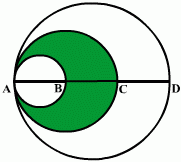

Pole figury zacieniowanej jest równe róznicy pól średniego okręgu o promieniu R = 3 i małego okręgu o promieniu r = 1,5.

P = pR² - pr² = p(R² - r²) = p(9 -  2,25) = 6,25p

Obwód figury zacieniowanej jest równe sumie obwoedów średniego okręgu o promieniu R = 3 i małego okręgu o promieniu r = 1,5.

Obw. = 2pR - 2pr = 2p(R - r) = 2p(3 - 1,5) = 3p

Joasia Konstanty