LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

Zadanie 12

Dany jest kwadrat o boku długości 4 cm. Z każdego wierzchołka jako ze środka poprowadzono koło o promieniu R = 4 cm. Wyznacz pole figury będącej częścią wspólną tych kół.

Rozwiązanie

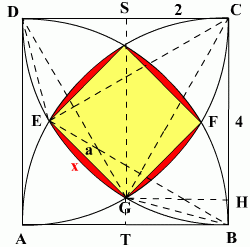Trójkąt DCG jest równoboczny, |CG|=4. Pole P szukanej figury jest równe

P = 4x + a2

PDGEC = PDGHC = ½ . 4 .2 = 4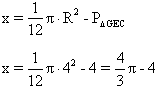

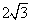Pole x jest równe różnicy pola wycinka kołowego GEC i pola trójkąta GEC:

|SG|2 = 42 - 22 = 12.  Stąd |SG| = oraz |TG| = 4 - .

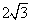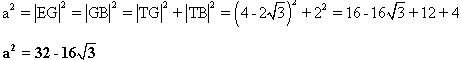
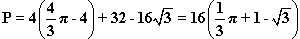
Odpowiedź

Pole figury jest równe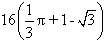  cm2, to jest około 5 cm2.

Marcin Liberacki