LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 12

W okrąg wpisano trójkąt ABC, gdzie |<A|=50o, |<B|=70o. Przez wierzchołek C poprowadzono styczną do okręgu przecinającą przedłużenie boku AB w punkcie D. Oblicz kąty trójkąta BCD.

Rozwiązanie

Dane: |<)BAC|= 50o i |<)ABC|= 70o   Szukana: |<)BDC|.
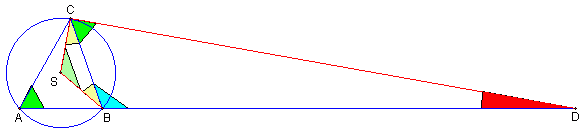
rysunek
Obliczenia:
  1. |<)BSC| = 2*|<)BAC|=2*50o = 100o,
    bo kąt środkowy jest zawsze dwa razy większy od kąta wpisanego opartego na tym samym łuku.
  2. Trójkąt BCS jest równoramienny,
    bo odcinki BS i CS są promieniami okręgu.
  3. |<)SCB|= |<)SBC| = (180o - 100o)/2 = 40o
  4. |<)SCD| = 90o,
    bo promień poprowadzony do punktu styczności jest zawsze prostopadły do stycznej.
  5. |<)BCD| = 90o - |<)SCB| = 90o - 40o = 50o
  6. |<)DBC| = 180o - |<)ABC| = 180o - 70o = 110o
  7. |<)BDC| = 180o - |<)CBD| - |<)BCD| = 180o - 110o - 50o = 20o
Odpowiedź: Kąty w trójkącie BDC ma miary: 110o, 20o i  50o.