LIGA ZADANIOWA UMK W TORUNIU 2000/2001

PREZENT WAKACYJNY

Zadanie 13

W kwadracie ABCD punkty E i F są odpowiednio środkami boków AD i CD, natomiast G jest punktem przecięcia odcinków CE i BF. Pokazać, że trójkaty ABG i AGD są równoramienne.

Rozwiązanie

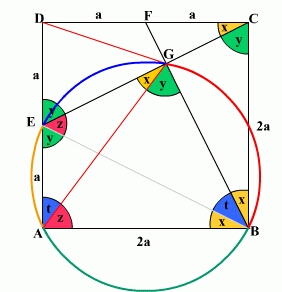
Trójkąty ABE, BCF i CDE są przystające ponieważ przy kątach prostych mają boki tej samej długości a i 2a. Stąd kąty w tych trójkątach x i y są odpowiednio równe.

W trójkącie BCF suma kątów x i y jest równa 90°, stąd trzeci kąt CGB ma 90°.

W czworokącie ABGE suma kątów przeciwległych przy wierzchołkach A i G jest równa 90°+90°=180°, więc można na nim opisać okrąg. Kąty oparte na tych samych łukach są przystajace i zaznaczyłem je odpowiednio tymi samymi kolorami.

Teraz możemy wyliczyć, że:

t = 90°-z i z = 180°-2y więc t = 90° - (180°-2y) = 2y - 90°.

Stąd w trójkącie ABG mamy:

t + x = 2y - 90° + x = (y + x) - 90° + y = 90° - 90° + y = y.

Zatem trójkąt ABG jest równoramienny i w związku z tym |AB|=|BG| = 2a.
Wynika z tego dodatkowo, że trójkąt DGA jest też równoramienny, bo |AD|=|BG|=2a.