Koło

ZADANIE 13

Oblicz miary kątów trójkąta równoramiennego, którego wierzchołki leżą na okręgu wiedząc, że jeden z boków jest oparty na 1/5 długości okręgu.

ROZWIĄZANIE

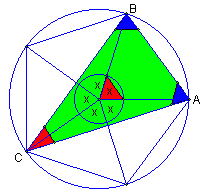
Oznaczam wierzchołki trójkąta jak na rysunku.
Obliczam miarę x kąta środkowego opartego na 1/5 okręgu. 5x = 360^o
x = 72^o
Kąt <)C jest wpisany w okrąg i musi być 2 razy mniejszy od kąta środkowego opartego na 1/5 łuku, więc |<)C| = 36^o.
Kąty przy podstawie trójkąta równoramiennego są przystające i suma miar kątów w trójkącie jest równa 180^o, więc
|<)A| = |<)B| = (180^o - 36^o) / 2 = 72^o.

ODPOWIEDŹ

Kąty w tym trójkącie mają miary: 36^o, 72^o, 72^o.