- Niech E będzie środkiem przekątnej BD.
- Niech X będzie punktem przecięcia się prostej przechodzącej przez punkt E i równoległej do przekątnej C.
|
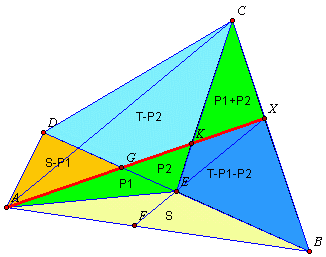 |
Pokażę, że prosta AX dzieli czworokąt ABCD na dwa wielokąty o równych polach
|
- Ponieważ E jest środkiem odcinka BD więc pola trójkątów AEB i AEC są równe oraz pola trójkątów BEC i CED są równe.
Oznaczmy S = PAEB = PAED i T = PBEC = PCED
- Odcinki EX i AC są równoległe więc pola trójkatów ACE i ACX są równe bo mają tę samą podstawę AC i wysokość.
Stąd PAKE = PACE - PAKC = PACX - PAKC = P
CKX
- Oznaczmy P1 = PDAEG i P2 = PDGEK
- PABX = S + (P1 + P2) + (T - P1 - P2) = S + T
PAXDC = (S - P1) + (T - P2) + (P1 + P2) = S + T
Stąd PABX = PAXDC
|
