LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ETAP IV -
ZADANIA NIESPODZIANKI
DLA KLAS VI SZKÓŁ PODSTAWOWYCH I KLAS I GIMNAZJUM
Zadanie 15
Mrówka musi jak najszybciej przebyć drogę od punktu A do punktu B po bokach siatki kwadratowej, unikając krawędzi zamalowanego kwadratu. Ile ma możliwych dróg?
Rozwiązanie
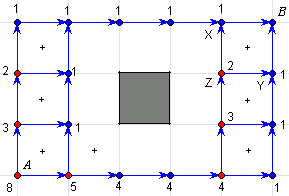
- Mrówka może wędrować po siatce tylko w górę lub w prawo by iść najkrótszą drogą. Liczbę dróg będę liczył od końca czyli od punktu B.
- Z punktów X i Y mrówka może dojść do punktu B jedną drogą. Skoro z punktu Z może dojść do punktów X i Y, więc z punktu Z może dojść do B w sumie dwiema drogami (1+1="2)." Rozumując tak samo dalej, zaznaczam przy każdym punkcie na rysunku liczbę dróg, które prowadzą z tego punktu do punktu B.
Rozwiązanie
Ostatecznie z punktu A do punktu B prowadzi 8 dróg.

