LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 17
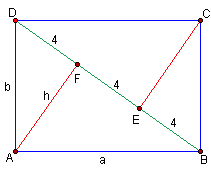
Z wierzchołków A i C prostokąta ABCD poprowadzono proste prostopadłe do przekątnej BD. Proste te dzielą przekątną na 3 równe części o długości 4cm każda. Oblicz długość boków prostokąta.Rozwiązanie
 |
|DF|=|EF|=|EB|=4cm |
| (1) Trójkąt ABF jest prostokątny, więc | a2 = h2 + 82. |
| (2) Trójkąt ADF jest prostokątny, więc | b2 = h2 + 42. |
| (3) Trójkąt ABD jest prostokątny, więc | a2 + b2 + 122. |
| Do równania (3) podstawiam wyniki (1) i (2): | h2 + 82 + h2 + 42 = 122 |
| 2h2 = 64 | |
| h2 = 32 | |
| Wstawiam wynik h2 = 32 do równania (1): | a2 = 32 + 82 = 96 = 16 . 6 |
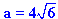 | |
| Wstawiam wynik h2 = 32 do równania (2): | b2 = 32 + 42 = 48 = 16 . 3 |
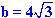 | |
Odpowiedź
Długości boków prostokąta wynoszą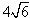 i
i 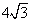 .
.
Agnieszka Osmoła