LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 16

W okręgu przeprowadzono trzy cięciwy tak, aby utworzyły one trójkąt ABC. Odcinek CO dzieli kąt ACB w stosunku 1:2. Kąt AOB wynosi 150 0

Rozwiązanie:

|<)AOB|=1500 wtedy i tylko wtedy gdy |<)ACB|=750.
Odcinek CO dzieli kąt ACB w stosunku 2:1, więc

|<)ACO| =2 * |<)BCO|
|<)ACO| + |<)BCO| = |<)ACB|
2 * |<)BCO| + |<)BCO| = 750
3 * |<)BCO|=750
|<)BCO| = 250
|<)ACO| = 2 * 250
|<)ACO| = 500

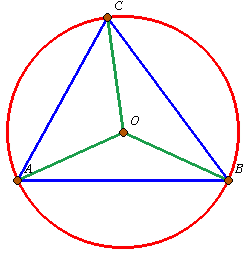
 Ładny, no nie?
Trójkąt AOC jest równoramienny (ramionami są promienie), więc:

|<)CAO| = |<)ACO| = 500

Trójkąt BCO jest równoramienny, więc:

|<)OBC| = |<)BCO| = 250

Kąt środkowy jest dwa razy większy od wpisanego:

|<)AOC| = 1800 - 2*500 = 800, stąd |<)ABC| =400
|<)BOC| = 180 0 - 250 = 1300, stąd |<)CAB|= 650

 Odpowiedź: Kąty wewnętrzne mają miary: 650, 400 i 750.