LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

ZADANIE 18

W trójkącie długości boków są równe 25, 25 i 40. Oblicz pole tego trójkąta oraz długości jego środkowych.

ROZWIĄZANIE:

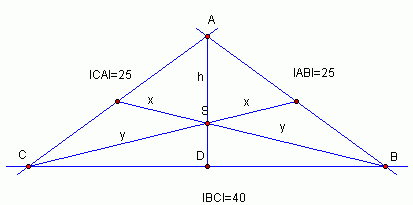
Rozmiar: 2716 bajtów


Pole=a . h : 2
Z twierdzenia Pitagorasa dla trójkąta DBA obliczamy wysokość
h2 + 202 = 252
h2 + 400 = 625 /- 400
h2 =225
h=15

P= 40 . 15 : 2
P=300
Z twierdzenia, że środkowe dzielą odcinek w stosunku 2:1 mierząc od wierzchołka możemy obliczyć środkowe
Jeżeli h = 15 to |DS|=5
202 + 52 = y2
200 + 25 = y2
y2 = 225
y = 15
y to 2:3 długości środkowej x+y, czyli x = 1:3 długości środkowej, więc jeżeli y =15 to x = 7,5.
Środkowa ma zatem długość
22,5


ODPOWIEDŹ:
Pole trójkąta równa się 300 cm2. Środkowe mają długości 22,5 cm, 22,5 cm i  15 cm.

Joasia Płachcińska