Graniastosłupy
| n="2k+2 |
| k="5 |
LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS I GIMNAZJUM
Zadanie 17
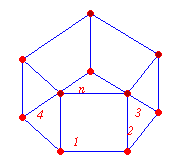
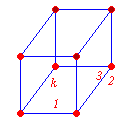
Z dwóch graniastosłupów pierwszy ma dwa razy więcej ścian niż drugi i o 21 krawędzi więcej niż drugi. Jakie wielokąty są podstawami tych graniastosłupów?Rozwiązanie
Graniastosłupy | ||
| I | II | |
 |  | |
| n-krawędzi w podstawie | k-krawędzi w podstawie | |
| n+2-liczba ścian | k+2-liczba ścian | |
| 3n-wszystkie krawędzie | 3k-wszystkie krawędzie | |
| WIADOMO, ŻE: | ||
| n+2="2(k+2) | 3n="3k+21 | |
| n+2="2k+4 | 3n="3k+21 | |
| 3(2k+2)=3k+21 | |
| 6k+6="3k+21 | ||
| 3k="15 | ||
| ||
Jeżeli
n="2k+2," a k="5," to:
n="2
n="12
Odpowiedź
Podstawami tych graniastosłupów są dwunastokąt i pięciokąt.