LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 17
W trapezie równoramiennym ABCD, w którym |AD|=|BC|=|CD| przekątna AC jest prostopadła do boku BC. Oblicz miary kątów tego trapezu.Rozwiązanie
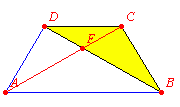
Trójkąty BCD i ACD sa przystające (bo mają boki tej samej długości) i są równoramienne. Zatem kąty CDB, DCA, CBD i CAD są równe.
Ponadto kąty naprzemianległe CDB i ABD oraz DCA i BAC są równe.
Zatem na sumę kątów w trapezie 360° składa się 6 kątów trównych i dwa kąty proste.
Od 360° odejmuję 180° (dwa kąty proste) i dzielę wynik na 6. Otrzymuję, że wymienione kąty równe BAC, CAD, ABD, DBC, ACD i BDC mają po 30°.
Stąd łatwo już wyliczyć, że kąty BAD i ABC mają po 60°, a kąty BCD i CDA mają po 120°.
Odpowiedź
Miary kątów w trapezie wynoszą 60°, 60°, 120° i 120°.Joasia Płachcińska