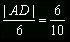LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 20
W trójkącie prostokątnym przyprostokątne maja długości 6cm i 8 cm. Oblicz długości odcinków, na które dzieli przeciwprostokątną wysokość opuszczona z wierzchołka kąta prostego.
Rozwiązanie
 |BA|=6 cm
|BA|=6 cm
|BC|=8 cm
Aby obliczyć przeciwprostokątną musimy skorzystać z tw. Pitagorasa.
|BA|2+|BC|2=|AC|2
|AC|2=36+64
|AC|=10 cm
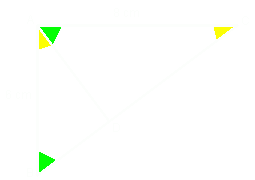
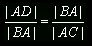
Możemy zauważyć, że trójkąt ABC jest podobny do trójkąta ABD.
Więc możemy utworzyć zależność, dzięki której obliczymy odcinek AD:
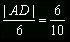
|AD|=3,6 cm
Teraz musimy obliczyć drugi odcinek:
|DC|=|AC|-|AD|
|DC|=10-3,6
|DC|=6,4 cm
Odpowiedź
Wysokość w tym trójkącie dzieli przeciw prostokątną na odcinki o długości 3,6 cm i 6,4 cm.
Paweł Rybacki
 |BA|=6 cm
|BA|=6 cm