LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 19

Przyprostokątne trójkąta prostokątnego mają długości 3 cm i 6 cm. Oblicz długość promienia okręgu o środku leżącym na przeciwprostokątnej i stycznego do obu przyprostokątnych.

Rozwiązanie

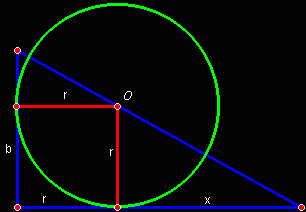
Z rysunku wynika, że:
r + x = 6
x = 6 - r

Największy trójkąt jest podobny do trójkąta o przyprostokątnych r i x, ponieważ te trójkąty mają te same miary kątów. Stosunki odpowiednich boków w trójkątach podobnych są równe, więc x : r = 6 : 3. Stąd
x : r = 2
Mnożę obie strony równania przez r
x = 2r
Za x podstawiam 6 - r
6 - r = 2r
Dodają do obu stron równania r
6 = 3r
Dzielę obie strony równania przez 3
2 = r

x + r = 6

Odpowiedź

Promień okręgu wpisanego w trójkat prostokątny, którego środek leży na przyprostokątnej wynosi 2 cm.