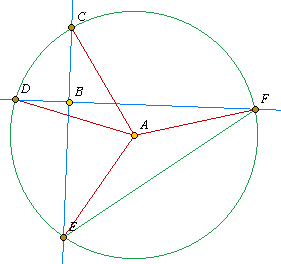
Kolorem czerwonym zostały oznaczone ramiona kątów środkowych opartych na łukach wyznaczonych przez te proste prostopadłe.
LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 20
Dwie proste prostopadłe dzielą okrąg na cztery łuki. Kąty środkowe oparte na łukach o mniejszych długościach mają miary 30o i 40o. Wyznacz miary kątów środkowych opartych na pozostałych łukach.Rozwiązanie
| Kolorem niebieskim zostały oznaczone dwie proste prostopadłe. Przecinają się one w punkcie B. Kolorem czerwonym zostały oznaczone ramiona kątów środkowych opartych na łukach wyznaczonych przez te proste prostopadłe. |  |
Po połączeniu punktów E i F powstał trójkąt prostokątny BEF.
Kąt DFE jest kątem wpisanym opartym na tym samym łuku co kąt DAE, więc: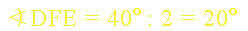
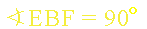 bo odcinek ED jest prostopadły do odcinka BF.
bo odcinek ED jest prostopadły do odcinka BF.
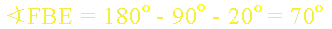
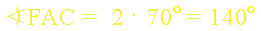
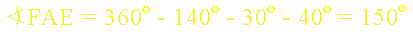
Odpowiedź
Kąty środkowe oparte na łukach na okręgu wyznaczonych przez dwie proste prostopadłe mają miary: 30 stopni, 40 stopni, 140 stopni i 150 stopni.
Monika Skocka kl.Ia