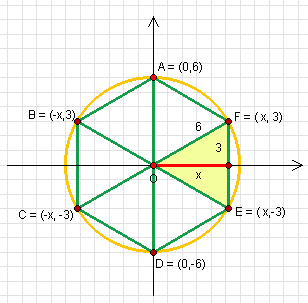
Wierzchołki sześciokąta wyznaczam poprzez odkładanie od punktu A = (0,6) odcinków długości 6 na okręgu o środku O = (0,0).
Z tw. Pitagorasa:
x2 = 62 - 32
x2 = 27
x2 = 9 . 3
x =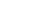 
Stąd sześciokąt ma wierzchołki
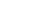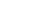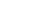A = (0, 6) B = (- , 3)C = (- , -3)D = (0 -6) E = ( , -3)F = ( , 3)
Obwód sześciokąta
OB = 6 * 6 = 36
Pole tego sześciokąta jest równe sumie pól sześciu trójkątów równobocznych, na które można podzielić ten sześciokąt.
Pole jednego z tych trójkątów można obliczyć ze wykorzystując wzór Herona:
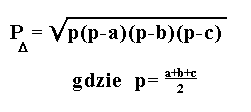
A więc pole sześciokąta wynosi:
