Rozwiązanie
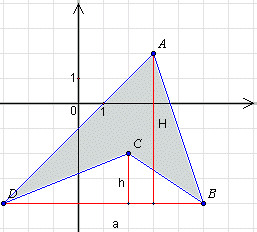
| Pole czworokąta ABCD jest różnicą pól trójkątów DBA i DBC: PABCD = PDBA - PDBC PABCD = (1/2) . a . H - (1/2) . a . h PABCD = (1/2) . 8 . 6 - (1/2) . 8 . 2 PABCD = 24 - 8 PABCD = 16 |
 |
Odpowiedź
Pole czworokąta wynosi 16 jednostek kwadratowych.