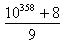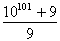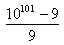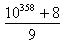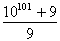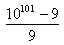LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
ZADANIE 21
Pytanie:
Które z poniżej podanych ułamków przedstawiają l. naturalne?
Aby ułamek przedstawiał l. naturalną to licznik musi być podzielny przez mianownik, tj. licznik musi być podzielny przez 9.
Zawsze przy potęgowaniu liczby 10 jest tak, że wynik potęgowania jest równy 100....0.
Liczba jest podzielna przez 9 jeżeli suma jej cyfr jest podzielna przez 9.
W przykładzie a, suma cyfr licznika jest równa 9, bo 1+0...0+8="9," a więc liczba z przykładu a jest naturalna.
W przykładzie b, suma cyfr licznika jest równa 10, bo 1+0...0+9="10," a 10 nie jest podzielne przez 9, więc liczba z przykładu b nie jest naturalna.
W przykładzie c, suma cyfr licznika jest równa 11, bo 1+0...0+9+1="11" a to też nie jest podzielne przez 9.