LIGA ZADANIOWA UMK W TORUNIU 2000/2001
ZADANIA KONKURSOWE Z ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 6
Wyznacz odległość między środkami okręgu wpisanego i okręgu opisanego na trójkącie, którego boki mają długości 10 cm, 10 cm i 16 cm.
Rozwiązanie
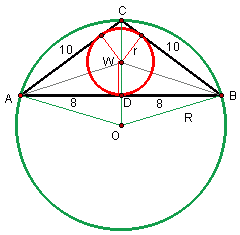
Trzeba policzyć długość odcinka WO.
- Z tw. Pitagorasa |CD|2=102-82=36
Stąd |CD|=6
- Pole P trójkąta ABC można policzyć na 2 sposoby:
P="(1/2)×|AB|×|CD|=(1/2)×16×6=48
P="(1/2)×|AB|×r+(1/2)×|BC|×r+(1/2)×|CA|×r=18×r
Stąd 18×r="48," więc |WD| = r="8/3
- Z tw. Pitagorasa
|OD|2+82 = R2
|OD|=R-6
(R-6)2+82 = R2
R2-12R+36+64="R2
12R="100
R="25/3
|OD|=R-6="7/3"
- |WO|=|WD|+|DO|=8/3+7/3="5"
Odpowiedź
Odległość między środkami okręgów wynosi 5 cm.
