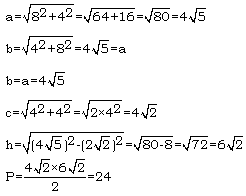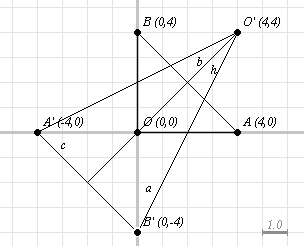
Dany jest trójkąt AOB, gdzie A = (4;0), B = (0;4) i O = (0;0). Niech A1 będzie obrazem punktu A w symetrii osiowej względem prostej OB, B1 obrazem B w symetrii osiowej względem prostej OA i O1 obrazem punktu O w symetrii osiowej względem prostej AB. Wyznaczyć pole trójkąta O1A1B1.
Rozwiązanie
Na rysunku:
A1 = A',
B1 = B',
O1 = O'.
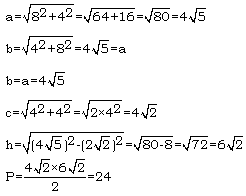
Odpowiedź
Pole trójkata O1A1B1 jest równe 24 jednostki kwadratowe.
