Zadanie 3
W okrąg wpisano trójkąt ABC. Wiadomo, że |<)A|=40°, |<)B|=80°. Przez wierzchołek C poprowadzono styczną do okręgu. Styczna ta przecina przedłużenie boku AB w punkcie D. Oblicz kąty trójkąta BCD.Rozwiązanie
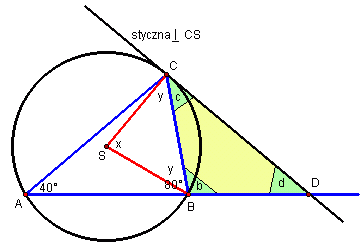
- Kąt środkowy x jest dwa razy większy od kąta wpisanego (BAC) opartego na tym samym łuku:
x = 2×40° = 80°. - W trójkącie równoramiennym BSC kąty przy podstawie są tej samej miary:
y = ½ (180°- x) = 50°. - Styczna jest prostopadła do promienia w punkcie styczności C:
c = 90° - y = 40°. - Kąty ABC i DBC są przyległe:
b = 180° - 80° = 100°. - Suma kątów w trójkącie (BCD) jest równa 180°:
d = 180° - (b + c) = 40°.
Odpowiedź
Kąty trójkąta BCD mają miary: 100°, 40°, 40°.Monika Boniecka