LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA Z PREZENTU WAKACYJNEGO
Zadanie 3
Ściany graniastosłupa prawidłowego czworokątnego mają powierzchnię:100 cm2 lub 400 cm2. Oblicz objętość tego graniastosłupa.
Przygotowanie do rozwiązania zadania:
Graniastosłup prawidłowy czworokątny to wielościan ograniczony dwiema ścianami (podstawami) w kształcie kwadratów i czterema ścianami (bocznymi) w kształcie prostokątów.
Objętość graniastosłupa prawidłowego czworokątnego wyraża się wzorem:
V = a 2 × h
Rozwiązanie:
Aby rozwiązać to zadanie musimy rozważyć cztery przypadki tzn.:
pierwszy - podstawy i ściany boczne mają powierzchnię 100 cm 2,
drugi - podstawy i ściany boczne mają powierzchnię 400 cm 2,
trzeci - podstawy mają powierzchnię 100 cm2, a ściany boczne 400 cm 2,
czwarty - podstawy mają powierzchnię 400 cm 2, a ściany boczne 100 cm 2.
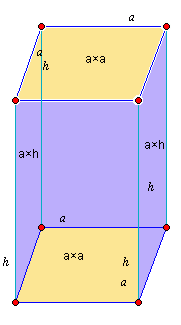 | W graniastosłupie prawidłowym czworokątnym zaznaczyłam podstawy kolorem różowym, a ściany boczne kolorem fioletowym.
Ppodstawy= a 2
Pścian bocznych = a × h |
Aby dowiedzieć się jaką objętość ma ta bryła należy dostosować się do wyżej wymienionych czterech przypadków.
Przypadek 1:
| a2 = 100 cm2 | | a × h = 100 cm2 |
| a = 10 cm 2 | | h = 100 : 10 = 10 cm |
V = a2 × h = 102 × 10 = 100 × 10 = 1000 cm3
Przypadek 2:
| a2 = 400 cm2 | | a × h = 400 cm 2 |
| a = 20 cm | | h = 400 : 20 = 20 cm |
V = a2 × h = 202 × 20 = 400 × 20 = 8000 cm3
Przypadek 3:
| a 2 = 100 cm 2 | | a × h = 400 cm 2 |
| a = 10 cm | | h = 400 : 10 = 40 cm |
V = a 2 × h = 102 × 40 = 100 × 40 = 4000 cm3
Przypadek 4:
| a2 = 400 cm 2 | | a × h = 100 cm2 |
| a = 20 cm | | h = 100 : 20 = 5 cm |
V = a2 × h = 202 × 5 = 400 × 5 = 2000 cm 3.
Odp. Graniastosłup którego powierzchnie ścian wynoszą 100 cm2 lub 400 cm 2, może mieć objętość 1000, 8000, 4000 lub 2000 cm 3.
Monika Boniecka

