LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA Z PREZENTU WAKACYJNEGO

Zadanie 5

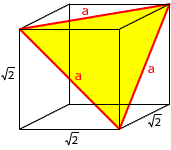
Oblicz pole trójkąta będącego przekrojem sześcianu 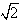o krawędzi .

Rozwiązanie

Ponieważ przekątna w kwadracie o długości 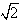wynosi 2, to dany trójkąt ma wymiary równe 2.

Z tw. Pitagorasa:

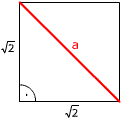W trójkącie równobocznym wysokość opada na podstawę ją na pół.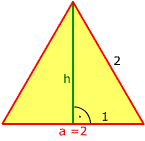
Wysokość trójkąta liczymy też z tw. Pitagorasa:

h2 + 12 = 22
h2 + 1 = 4
h2 = 3

Obliczamy pole P danego trójkąta:

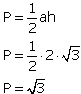
Odpowiedź

Pole trójkąta jest równe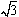 pierwiastek z trzech.

Andrzej Burek