LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS I GIMNAZJUM

Zadanie 6

Oto zadanie historyczne, liczące 4000 lat, zapisane na tzw. Papirusie Rhinda odnalezionym we wnętrzu jedenj z piramid w roku 1853.

Rozdziel 100 miar ziarna między pięciu robotników tak, aby drugi otrzymała o tyle miar więcej od pierwszego, o ile trzeci otrzymała więcej od drugiego, czwarty od trzeciego i piąty od czwartego. Oprócz tego dwóch pierwszych robotników razem powinno otrzymać siedem razy mniej ziarna niż trzej pozostali. Ile miar ziarna otrzymał każdy z robotników?

Rozwiązanie

Pierwszy robotnik dostał:	x miar.	Razem robotnicy dostali 100 miar. 5x + 10r = 100 x + 2r = 20 x = 20 - 2r
Drugi robotnik dostał:	x + r miar
Trzeci robotnik dostał:	x + 2r miar.
Czwarty robotnik dostał:	x + 3r  miar.
Piąty robotnik dostał:	x + 4r miar.

W drugiej tabeli wstawiam zamiast x wyliczone 20 - 2r.

Pierwszy robotnik dostał:	20 - 2r miar.	Dwóch pierwszych robotników razem powinno otrzymać siedem razy mniej ziarna niż trzej pozostali. 7(20 - 2r + 20 - r)= 20 + (20 + r) + (20 + 2r) 7(40 - 3r) = 60 + 3r 280 - 21r = 60 + 3r 24r = 220 r = 9 + (4/9)
Drugi robotnik dostał:	20 - r miar
Trzeci robotnik dostał:	20 miar.
Czwarty robotnik dostał:	20 + r  miar.
Piąty robotnik dostał:	20 + 2r miar.

W trzeciej tabeli wstawiam zamiast r wyliczone 9 + (4/9).

Pierwszy robotnik dostał:	20 - 2r = 20 - 2(9 + 4/9) = 20 - (18 + 8/9) = 1 + 1/9 miar.
Drugi robotnik dostał:	20 - r = 20 - (9 + 4/9) = 10 + 5/9 miar.
Trzeci robotnik dostał:	20 miar.
Czwarty robotnik dostał:	20 + r = 20 + (9 + 4/9) = 29 + 4/9 miar.
Piąty robotnik dostał:	20 + 2r = 20 + 2(9 + 4/9) = 20 + (18 + 8/9) = 38 + 8/9 miar.

Odpowiedź

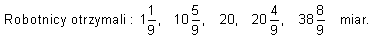
Radek Cywiński