LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA Z PREZENTU WAKACYJNEGO

Zadanie 13

Niech a, b, c będą długościami boków trójkąta. Wykaż, że

Rozwiązanie

W trójkąt wpisujemy okrąg, a następnie prowadzimy promienie do punktów gdzie okrąg styka się z bokami trójkąta (pod kątem prostym).
Trójkąty APS i ARS są przystające bo oba są prostokątne i mają po dwa boki parami równej długości:
|AS|=|AS| i |SP|=|SR|=r. Więc |AP|=|AR|=
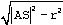
Podobnie |BP|=|BQ| i |CQ|=|CR|. 		Rysunek pomocniczy
Możemy więc oznaczyć:
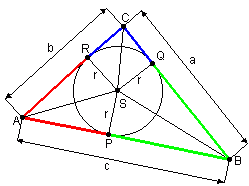
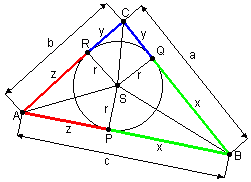
  • długości odcinków AP i AR jako z,
  • długości odcinków BP i BQ jako x,
  • długości odcinków CQ i CR jako y.
Przy tych oznaczeniach nierówność, którą mamy pokazać wygląda tak:
Czyli po redukcji:
Teraz napiszemy każdy wyraz po lewej stronie nierówności dwukrotnie, ale podzielimy przez 2, tak żeby wartość się nie zmieniła:
Teraz wystarczy tylko pokazać, że każdy z wyrazów po stronie lewej jest mniejszy bądź równy odpowiadającemu mu wyrazowi po stronie prawej. Zrobię to dla pierwszych składników po lewej i prawej stronie (reszta jest podobnie):

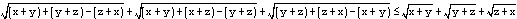
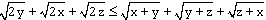
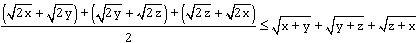
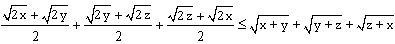
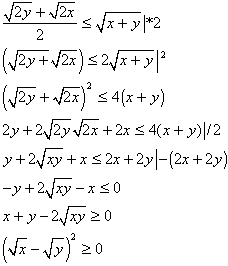
Ostatnia nierówność jest zawsze prawdziwa bo kwadrat liczby nieujemnej jest nieujemny. Tak więc i pierwsza nierówność musi być prawdziwa i podobnie wszytkie trzy odpowiednie nierówności są przwdziwe
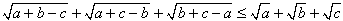Tym samym wykazałem, że:

.

Michał Janeczek