 .
.LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM
Zadanie 13
Liczba naturalna n jest równa sumie pewnych trzech różnych dzielników liczbyRozwiązanie
Załóżmy, że liczba n spełnia warunki zadania i, żen = a' + b' + c',
gdzie a', b', c' są różnymi dzielnikami liczbyNiech 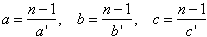 .
.
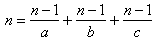 .
.
Poszukajmy teraz liczb a, b, c.
Wynieśmy najpierw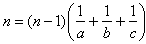
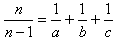
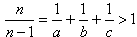 .
.
Możemy założyć, że 1 < a < b < c < n - 1.
Jeśli a ≥ 3, to b ≥ 4 i c ≥ 5, i stąd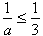 ,
, 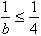 ,
, 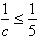 .
.
Ale wtedy 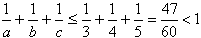 .
.
a to jest niemożliwe, bo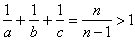 .
.
Przypuśćmy, że b ≥ 4.
Wtedy c ≥ 5 i 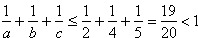
To jest niemożliwe, wiec b = 3.
Załóżmy, że c = 4.
Wtedy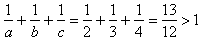
czyli c może równać się 4.
Załóżmy teraz, że c = 5.
W takim wypadku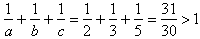 .
.
Wynika z tego, że c może równać się 5.
Zobaczmy czy c może równać się 6.Dla c = 6 mamy 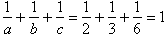 .
.
To oznacza, że c nie może się równać 6 i nie może być większe niż 6.
Ostatecznie otrzymaliśmy więc, że a = 2, b = 3, c = 4 lub a = 2, b = 3, c = 5.
Pozostaje wyznaczyć szukane liczby n.
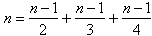
12n = 6n - 6 + 4n - 4 + 3n - 3
- n = - 13
n = 13
Sprawdźmy to: n = 13, n - 1 = 12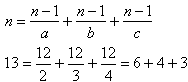
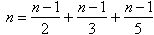
30n = 15n - 15 + 10n - 10 + 6n - 6
- n = -31
n = 31
Sprawdźmy i tę liczbę: n = 31, n - 1 = 30.
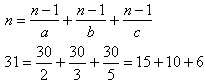
Ponownie brak zastrzeżeń.
Odpowiedź:
Wszystkie możliwe liczby n spełniające warunki zadania to 13 i 31.Michał Janeczek