Liga Zadaniowa UMK

LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 13

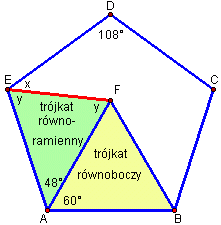
Dany jest pięciokąt foremny ABCDE. Punkt F leży wewnątrz pięciokąta i ma taką własność, że trójkąt ABF jest równoboczny. Oblicz miarę kąta DEF.

ROZWIĄZANIE

Na matematyce uczono nas jaka jest suma miar w różnych wielokątach. Powinniśmy zatem wiedzieć, że suma miar kątów wewnętrznych w n-kacie jest równa

(n-2)×180°
----------
     n

Tak więc suma miar kątów w pięciokącie (n=5) będzie wynosić 540°. Pięciokąt foremny ma wszystkie kąty równe (każdy po 108°) Obliczamy to w ten sposób: 540°:5=108°

Trójkąt ABF jest równoboczny i jak wiemy suma kątów w trójkącie równobocznym = 180°, dlatego każdy z jego kątów będzie miał 60°. Gdy od 108° odejmiemy 60° to zostanie nam 48°. Dlatego też kąt FAE będzie miał 48°. Trójkąt ABF jest równoramienny. Dlatego 2y + 48 = 180°, więc y = 66°. Tak więc x = 108° - y = 108° - 66° = 42°

Odpowiedź Kąt DEF ma 42°.

Marta Jankowiak