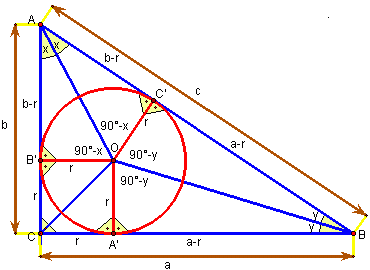
 1.Tak więc na początku wykonamy skomplikowany rysunek :) Na czerwono zaznaczymy promienie koła wpisanego w trojkąt.
1.Tak więc na początku wykonamy skomplikowany rysunek :) Na czerwono zaznaczymy promienie koła wpisanego w trojkąt. LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA Z PREZENTU WAKACYJNEGO
Zadanie 14
Niech r i R oznaczają odpowidnio promień okręgu wpisanego i opisanego na trójkącie prostokatnym. Wykaż, że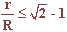
ROZWIĄZANIE
 1.Tak więc na początku wykonamy skomplikowany rysunek :) Na czerwono zaznaczymy promienie koła wpisanego w trojkąt.
1.Tak więc na początku wykonamy skomplikowany rysunek :) Na czerwono zaznaczymy promienie koła wpisanego w trojkąt.
2. Gdy się przyjrzymy można dostrzec kwadrat CA'OB', więc odcinek CA' będzie się równał długości promienia okregu. To samo dotyczy z odcinka.CB'.
3. Skoro CA' ma długość r, to A'C ma długość b - r, itd. ... .
4. Co najmniej od kilku lat powinniśmy wiedzieć, że dwusieczna kąta dzieli go na dwa takie same kąty. Dlatego też kąty przy wierzchołku A, oznaczone przez x są przystające. Tak więc na podstawie cechy przystawania trójkatów bkb (bok r, kąt 90°-x, bok AO) trójkąty AB'O i AC'O będą przystające. Zatem |AC'| = |AB' = b-r. Taka samo |BC'| = |BA'| = a-r.
5. Z powyższych uwag wynika, że c = a + b - 2r. Stąd 2r = a + b - c. Wniosek dla nas najważniejsz jest teraz następujący:
PROMIEŃ OKRĘGU WPISANEGO W TRÓJKĄT PROSTOKĄTNY WYRAŻA SIĘ WZOREM
PROMIEŃ OKREGU OPISANEGO NA TÓRJKĄCIE PROSTOKATNYM JEST RÓWNY POŁOWIE PRZECIWPROSTKĄTNEJ, A WIĘC WYRAŻA SIĘ WZOREM
|  |
A teraz zobaczymy, co oznacza nierówność podana w zadaniu:
| 1 | Mamy pokazać, że: | 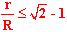 |
| 2 | Podstawiamy wzór na r i R: | 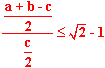 |
| 3 | Mnożymy licznik i mianownik "piętrowca" przez 2: | 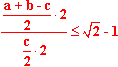 |
| 4 | Teraz trochę lepiej to wygląda: | 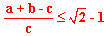 |
| 5 | Ułamek zamieniamy na różnicę dwóch ulamków: | 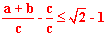 |
| 6 | Oczywiście c dzielone przez c równa się 1: | 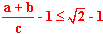 |
| 7 | Do obu stron równania dodajemy 1: | 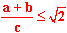 |
| 8 | Mnożymy obie strony przez c: | 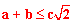 |
| 9 | Podnosimy lewą i prawą stronę do kwadratu: | 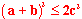 |
| 10 | Z lewej strony stosujemy wzór skróconego mnożenia, a z prawej tw. Pitagorasa: | 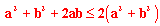 |
| 11 | Z prawej strony stosujemy rozdzielność mnożenia względem dodawania: | 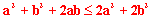 |
| 12 | Od obu stron równania odejmujemy a2 + b2: | 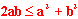 |
| 13 | Od obu stron równania odejmujemy 2ab: | 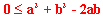 |
| 14 | Widzimy, że po prawa strona, to wzór skróconego mnożenia na (a-b)2: | 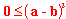 |
Ostatnia nierówność jest oczywiście zawsze prawdziwa bo kwadrat jakiejkolwiek liczby jest większy lub równy 0.
Widzimy więc, że pierwsza nierówność: 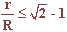 także musi być prawdziwa!
także musi być prawdziwa!
Marta Jankowiak