
LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU IV
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Zadanie 15
| Mrówka musi jak najszybciej przebyć drogę od punktu A do punktu B po bokach siatki kwadratowej, unikając krawędzi czarnego kwadratu. Ile ma możliwych dróg? |
|
Rozwiązanie
| Przy każdym punkcie, przez który może przejść mucha zaznaczyłem ile dróg prowadzi do tego punktu od punktu A. Ostateczne do punktu B prowadzi 8 dróg. | 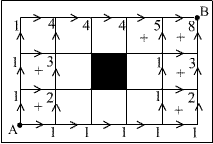 |
| Droga 1 | Droga 2 | Droga 3 | Droga 4 |
 |
 |
 |
 |
| Droga 5 | Droga 6 | Droga 7 | Droga 8 |
 |
 |
 |
 |
(C) by Wojtek Krzemiński 2002