LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 16

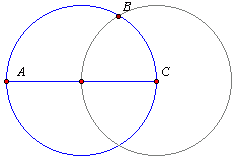
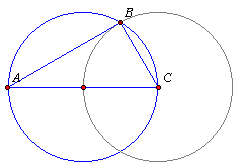
Na okręgu obierz trzy punkty A, B, C tak aby powstał trójkąt prostokątny, a miara kąta ostrego CAB wynosiła 30°. Oblicz miary kątów środkowych opartych na łukach wyznaczonych przez przyprostokątne AC i BC trójkąta ABC.

Rozwiązanie

1.

Rysujemy dowolny okrąg
i dowolną jego średnicą,
której końce oznaczamy literami A i C.

2.

Z punktu C zataczamy okrąg o promieniu równym promieniowi narysowanego okręgu. Punkt przecięcia się okręgów oznaczamy literą B.

3.

Łączymy odcinkami wierzchołki C i B oraz A i B.

W wyniku otrzymujemy trójkąt ABC, w którym

Kąt CAB ma miarę 30º

Kąt ABC ma miarę 90º

Kąt BCA ma miarę 60º

4.

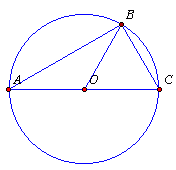
Kąt środkowy COB ma miarę 60°
gdyż jest dwa razy większy od kąta wpisanego CAB o mierze 30°.

Kąt środkowy BOA ma miarę 120°
bo jest dwa razy większy od kąta wpisanego BCA o mierze 60°.

Marcin Kusz