LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
ZADANIE 18
W okrąg wpisano trójkąt ABC, gdzie |<)A|=50°, |<)B|=70°. Przez wierzchołek C poprowadzono styczną do okręgu przecinającą przedłużenie boku AB w punkcie D. Oblicz kąty trójkąta BCD.ROZWIĄZANIE
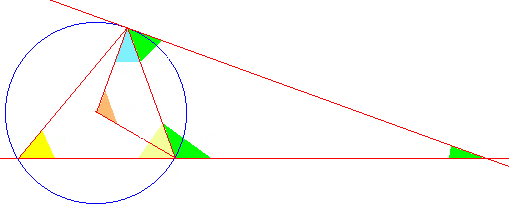
Rysunek do zadania wygląda tak:

Na początku mamy dane 50° i 70°.
Kąt środkowy jest 2 razy większy od kąta wpisanego
opartego na tym samym łuku:
|<)BSC| = 2×50° = 100°.
Trójkąt BSC jest równoramienny (jego ramionami są promienie okręgu) więc
|<)SCB| = (180° - 100°)/2 = 40°.
Promień SC jest prostopadły do stycznej SC, więc
|<)BCD| = 90° - 40° = 50°.
Kat DBC jest przyległy do kąta 70°, więc
|<)DBC| = 180° - 70° = 110°.
Suma katów w trójkącie (BDC) ma 180°, więc
|<)BDC| = 180° - 110° - 50° = 20°
ODPOWIEDŹ
Trójkąt BDC ma kąty 50°. 110° i 20°.
Tomek Nowak