LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS I GIMNAZJUM

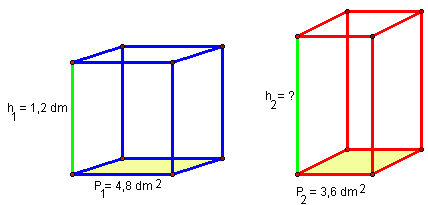
Pole podstawy figury a wynosi P1= 4,8 dm2
Wysokość figury a wynosi h1= 1,2 dm
Objętość figury a wynosi V1 = P1 × h1 = 4,8 × 1,2 = 5,76 dm3
Pole podstawy figury b wynosi P2= 3,6 dm2
Wysokość figury b jest niewiadomą h2= ? dm
Objętość figury b wynosi V2 = P2 × h2 = 3,6 × h2 = 5,76 dm3
| 3,6 × h2 = 5,76
h2 = 5,76:3,6 h2 = 1,6 |
Justyna Piotrowska